Key concepts from "The Words of Risk Analysis" by Stan Kaplan (Risk Analysis, v.17, n.4, 1997) including the delightful beginning:
Upon being informed that I would be expected to speak today I asked myself what I could say, in half an hour, that would be useful. Upon doing that I got an immediate answer. A voice in my head said, "Talk about the words." My first thought was that this would take more than one half hour. Second thought was: I can squeeze it, and I'd like to do it. Besides, since I don't hear voices all that often, maybe I should pay attention. So here goes.
... and the central definition of Risk, via three questions:
- What can happen? (What can go wrong?)
- How likely is it? (What is its frequency/probability?)
- What are the consequences? (What is the damage?)
... and then respectively using Si for the ith scenario (answering the first question), Li for the associated likelihood (second question), and Xi for the consequences (third question), the set of all triplets { (Si, Li, Xi) } is the Risk. Kaplan observes:
Notice that defined in this way, risk is not a number, nor is it a curve, nor a vector, etc. None of these mathematical concepts is "big" enough in general to capture the idea of risk. But the set of triplets, we find, is always big enough, and if we start out with that, it always gets us on the right track.
Once scenarios are defined, the likelihoods and consequences of the scenarios can be expressed as probability curves, defined by the evidence via Bayes Theorem. Kaplan says:
... To a Bayesian, this is not just another theorem. It's the fundamental law governing the evaluation of evidence.
To an extremist Bayesian, like myself, it goes deeper than that. It's not only the fundamental principle of logical inference, it's the very definition of logic itself. It's what we mean by logical, rational thinking. ...
Kaplan explains further how to gather and analyze evidence from experts:
By the way, this point of view guides us on how to deal with experts. It tells us we should never ask an expert for his opinion. What we want from an expert is, his experience, his information, his evidence.
It also guides us on how to deal with a group of experts. We must first convert the question to a quantitative form, e.g., "What is the numerical value of this parameter F?" We then ask the experts "What evidence do we have relevant to this question?" As they answer we write down, and enumerate, a list of all the relevant evidence items available. We write down exactly what happened as distinct from our interpretations of what happened. We work over this list with the group until we obtain what we can call the "consensus body of evidence." At this point we apply Bayes' theorem to the list, item by item, at the end of which we have a consensus probability curve expressing what we collectively know about the value of F.
Kaplan goes on to discuss decisions, regulations, scenarios, and communications. He summarizes it all in his Figure 19, "How It All Fits Together". Neat!
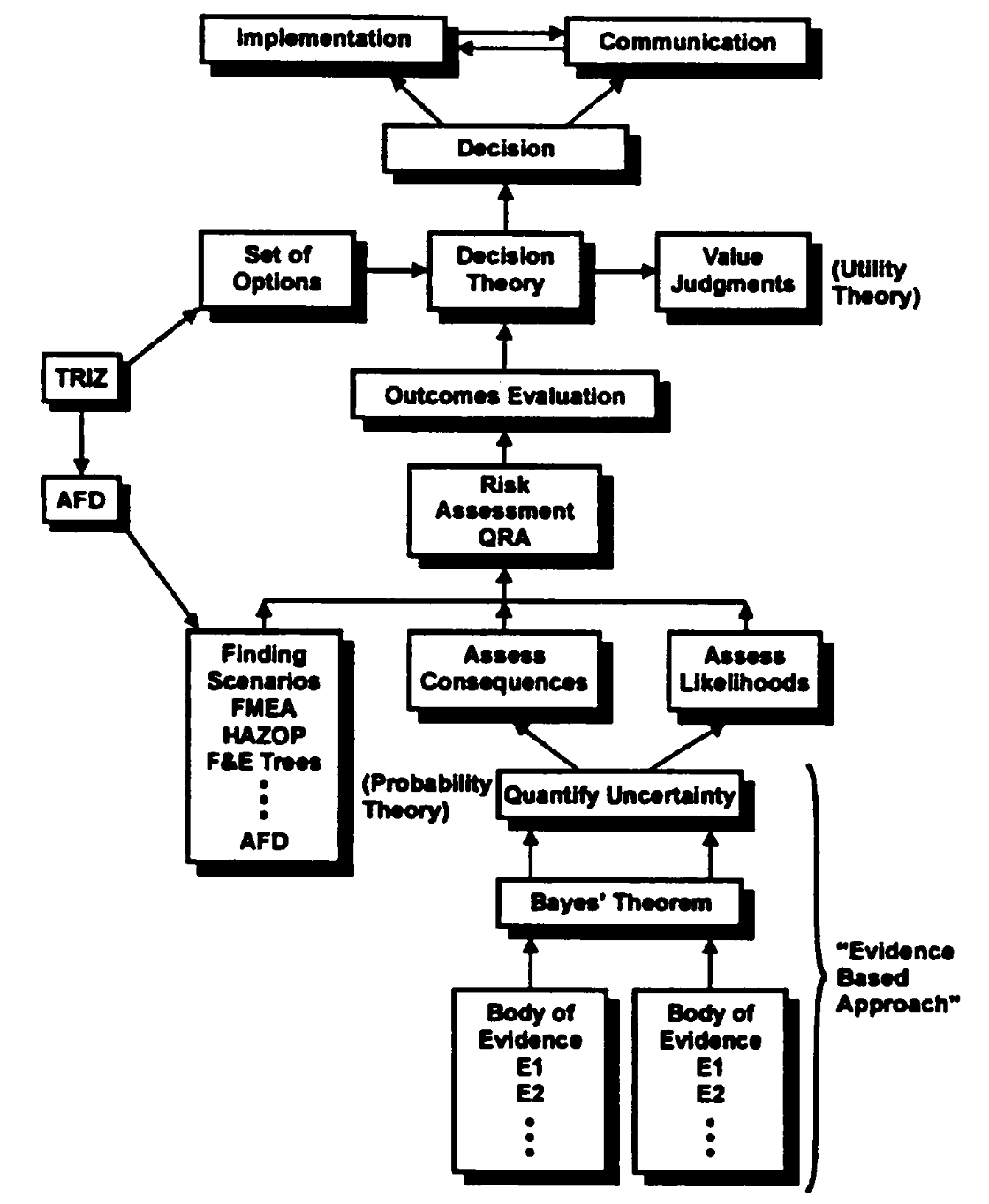
^z - 2022-12-22